Hans H. Diebner's Research
Turing pattern in a two-dimensional diffusively coupled oscillator array
Please have a look at the reactive installation Liquid Perceptron, which has been developed within the scope of "performative science" and has been several times successfully on show.
The network of diffusively coupled nonlinearer oscillators obeys the differential equations:
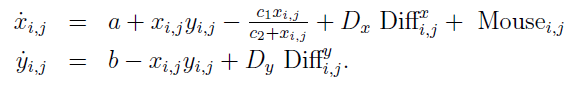
with i = 1, ..., 160 und j = 1, ... , 140. Each of the 160 X 140 oscillators is two-dimensional (i.e., variables x and y). The influx parameter a can be controlled with the slider and is pre-set to a = 0.062. Further parameter values: b = 0.12; c1 = 0.502; c2 = 0.1; Dx = 0.3; Dy = 0.01. The diffusion terms Dx and Dyare given by:
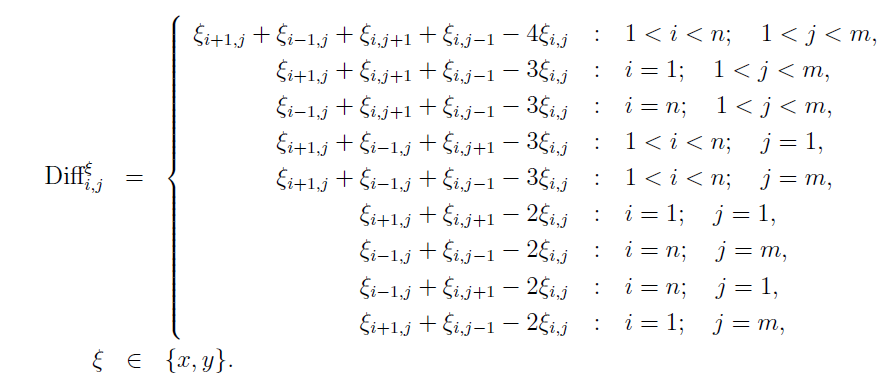
The interaction term "Mouse" in the above formula becomes larger zero if the left mouse button is pressed and the mouse moved over the visualisation. In this case, those oscillators (pixels) (i,j) which are touched by the mouse cursor each receive a short impulse, i.e., an additional influx of the order 0.1 for a short time. Thus, Turing patterns in form of spiral waves as a result of synchronisation of neighbored oscillators are generated. The system is at the edge of self-excitation with default parameter value a = 0.062. An external stimulus (here mouse click and movement) pushes the system above the excitation threshold and eventually releases sustaining patterns. Lower values of parameter a lead to permanent self-excitation, whereas larger values only lead to a weak background oscillation (fluctuation). The most interesting state is just below self-excitation such that small stimuli are capable to excite the network.
Thanks to pixi.js